In this chapter, we provide evidence in support of the inferences that are directly related to measurement modeling and scoring decisions. VALLSS has both code-based and language tests, but only the code-based tests lend themselves to IRT-based scoring. In this chapter, we describe the analytical approach we took with each set of tests.

Code-Based Tests

Table 4 outlines the inferences we have made about the code-based tests. They are concerned with the appropriateness of the measurement model and scoring approach used to produce scores for VALLSS, how well the resulting scores reflect students’ growth over time, and how accurately the scores can be used to identify students at risk for developing reading difficulties.

Table 4.
Overview of Scoring Inferences, Assumptions, and Supporting Analyses

Inference 1: The measurement model used for scoring fits the VALLSS data

A primary assumption underlying VALLSS is that the vertical scale produces scores that represent the unidimensional construct of code-based literacy. This assumption, in turn, relies on multiple constituent assumptions, including that (a) items are strong/reliable indicators of the construct; (b) the items measure a unidimensional construct (in line with theory stemming from the science of reading); (c) the scores are reliable; (d) the ultimate model used to produce scores produces good fit between the model and the item responses; and (e) the measurement properties are consistent for all examinees.

Assumption 1.a: Items are strong/reliable indicators of the construct

To test this assumption, we estimated point-biserial correlations for all the items across the code-based subtests in the test forms for each grade (Table 5 shows the number of items in each subtest for each grade form). These correlations quantify the association between the score on the test and the response to a given item. As a student’s overall score increases, so too would we expect their probability of a correct response to increase for a given item. The forms for Kindergarten and Grades 1 and 2 each had three or fewer items with values less than 0.3, which is a widely accepted cutoff indicating that an item is not a reliable indicator (squaring the correlation suggests that less than 10% of the variance in the item response is explained by the test score, which proxies for the skill we want to quantify). We flagged these items for further consideration. In Grade 3, however, nearly all Segmenting Phonemes items were below the 0.3 cutoff. This indicated to us that there was likely a dimensionality issue at the higher grades, which we explored further via the confirmatory factor analysis (CFA) described in the following section. Considerations based on the content of VALLSS are addressed in Chapter 2.

Table 5.
Number of Code-based Items by Subtest and Grade

Assumption 1.b: The items measure a unidimensional construct.

We used three different CFA models to provide evidence that the code-based items at each grade level represent a single, unidimensional latent variable: (1) a one-dimensional model (1D model); (2) a model in which there were separate, but correlated, latent variables for each subtest represented at each grade level (Subtest model); and (3) a testlet model in which all items represented both a general latent variable and a latent variable specific to the targeted domain (alphabet knowledge, de/encoding, and phonological awareness) (Testlet model). We then compared the fit of the unidimensional model to the other, multidimensional models. Note that the testlet model is a more constrained version of the bifactor model. In each of these models, the items were treated as binary rather than continuous. We conducted these analyses separately by grade because the vertical scale design generated too much missingness (by design) to estimate multigroup CFA models. The fit statistics for each model are shown by grade in Table 6. While the subtest models typically had the best fit, differences were often marginal compared to the fit of the unidimensional model after removing Segmenting Phonemes and Letter Names (a choice discussed momentarily).

Given that a priori theory from reading experts suggest these code-based skills represent a unidimensional construct, we examined the subtest correlations from the subtest models to see which subtests may be diverging from the others and causing inadequate fit in the 1D models. In kindergarten (Table 7), the subtest correlations were generally very high, though the Letter Names and Segmenting Phonemes subtests had lower correlations with some of the other subtests. While the Letter Names subtest was only present in the kindergarten test, there were Segmenting Phonemes items in the test forms for all four grades. As the grade level increased, the correlations between the Segmenting Phonemes subtest and the other subtests decreased, with the correlations being less than 0.4 by Grade 3 (Table 8). Because the content team had speculated prior to our analyses that these subtests might function differently than the others, and given our results, we removed both the Letter Names and Segmenting Phonemes subtests from the vertical scale. The Letter Names subtest is now optional for teachers to administer, and the Segmenting Phonemes subtests are now optional for Grades 2 and 3. While Segmenting Phonemes is still required for Kindergarten and Grade 1 students, those items are not included in the vertical scale at any grade. By removing these sets of items, we were able to obtain acceptable fit statistics for a unidimensional model (Table 6). Additionally, the non-Segmenting Phonemes items with low point-biserial correlations (described in the previous section) had adequately high factor loadings in the final 1D model and did not need to be removed.

Table 6.
Confirmatory Factor Analyses Model Fit Statistics by Grade

Table 7.
Correlations for Kindergarten Subtests (Subtest model)

Table 8.
Correlations for Grade 3 Subtests (Subtest model)

Assumption 1.c: VALLSS produces reliable scores

Once we had determined which items to retain and examined the factor structure, we calculated Cronbach’s alpha for each grade level and obtained the values presented in Table 9. We also examined the marginal reliabilities for each grade that were calculated based on our IRT model described in the next section. These two sets of values were high enough to suggest that VALLSS scores are reliable and internally consistent.

Table 9.
Cronbach’s Alpha Values by Grade

Assumption 1.d: The measurement model has acceptable fit with the VALLSS item data

VALLSS test forms were designed to include linking items for each pair of adjacent grades and for each subtest. We calibrated the item parameters using a multigroup IRT model, where each grade level was its own group. The parameters for the linking items were constrained to be equal for both groups, which allowed us to place all items across the four grades onto the same IRT scale.  In the context of vertical scaling, we needed to make several decisions related to model specification. One of those decisions was whether to use a Rasch, 2-parameter logistic (2PL), or 3-parameter logistic (3PL) IRT model. Before modeling the item responses, we decided against use of a 3PL model because the students taking the test are generally young enough that guessing as a testing strategy is not a major concern. Further, there are no incentives for students to try to guess.

In terms of using Rasch versus 2PL, there are theoretical arguments for and against each. Arguments in favor of the Rasch model are that sum scores are a sufficient statistic for IRT-based scores and that the Rasch model possesses properties that are necessary but insufficient for building an equal-interval scale (Briggs, 2013). However, an important benefit of the 2PL model in the context of vertical scaling is that the 2PL permits additional flexibility in accounting for multidimensionality when difficulty is strongly related to dimensionality (Meng et al., 2025).  With these strengths in mind, we compared the AIC and BIC statistics for the Rasch and 2PL models, and the 2PL demonstrated better fit. Given the superior fit of the 2PL model coupled with concerns about mild departures from unidimenionsality in kindergarten, we opted for the 2PL model.

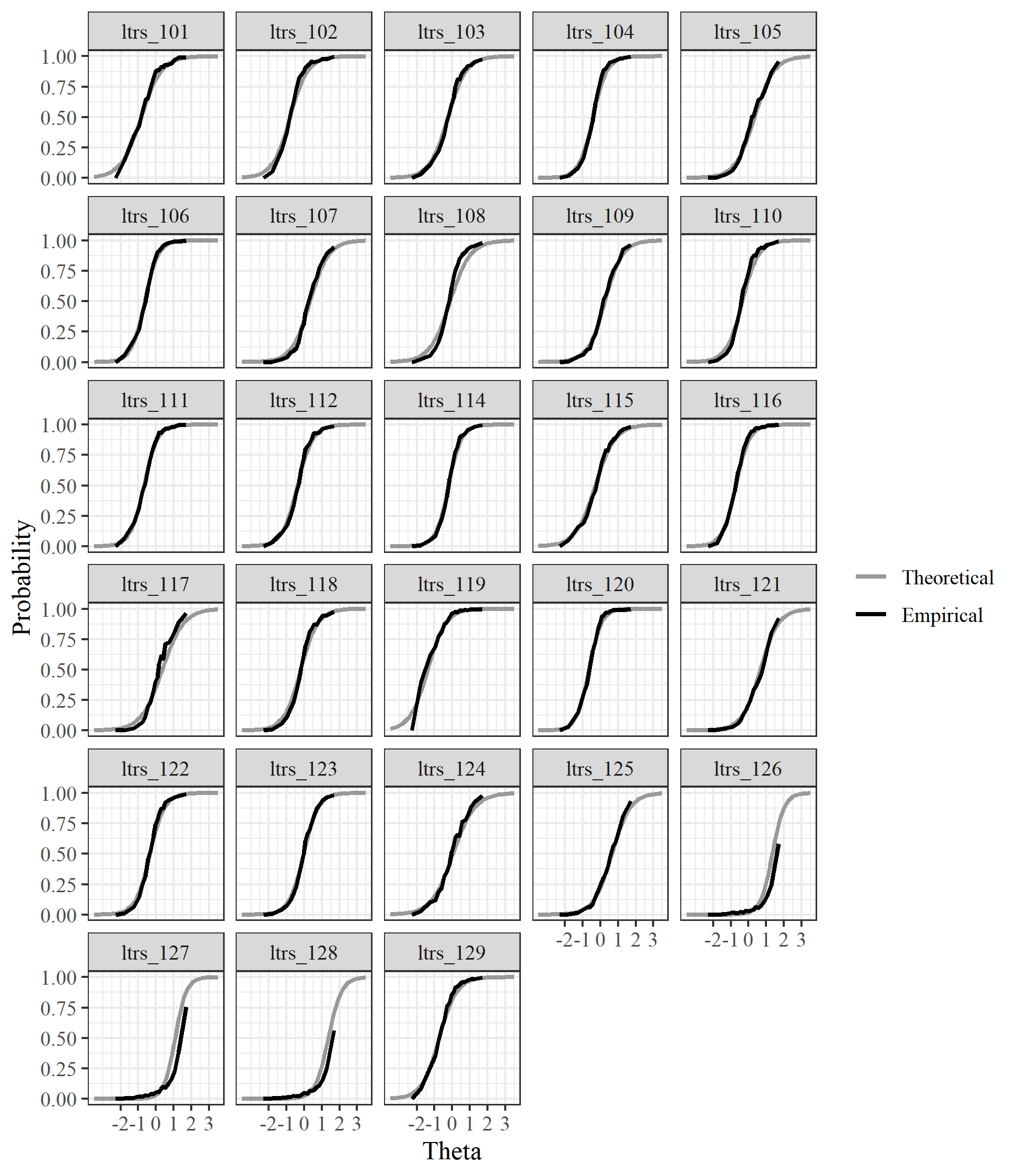
We also compared the empirical and theoretical (2PL) item characteristic curves for each item for both a 1D model and a testlet model (as described previously). The theoretical curves for the testlet model used the parameters for the general factor, which were constrained to be equal to those for the subtest-specific factors. The empirical and theoretical curves had a high degree of alignment for the 1D model, but several items at each grade level had substantial differences for the testlet model (see Figure 1 for the 1D curve comparisons for the Letter Sounds items in the Kindergarten test, as an example). These findings, in combination with the CFA model fit statistics (Table 6), provided further evidence supporting use of the 1D model with two subtests (Alphabet Names and Segmenting Phonemes) removed from the vertical scale.

Figure 1.
Theoretical vs Empirical Item Characteristic Curves for Letter Sounds Items on the Kindergarten Test

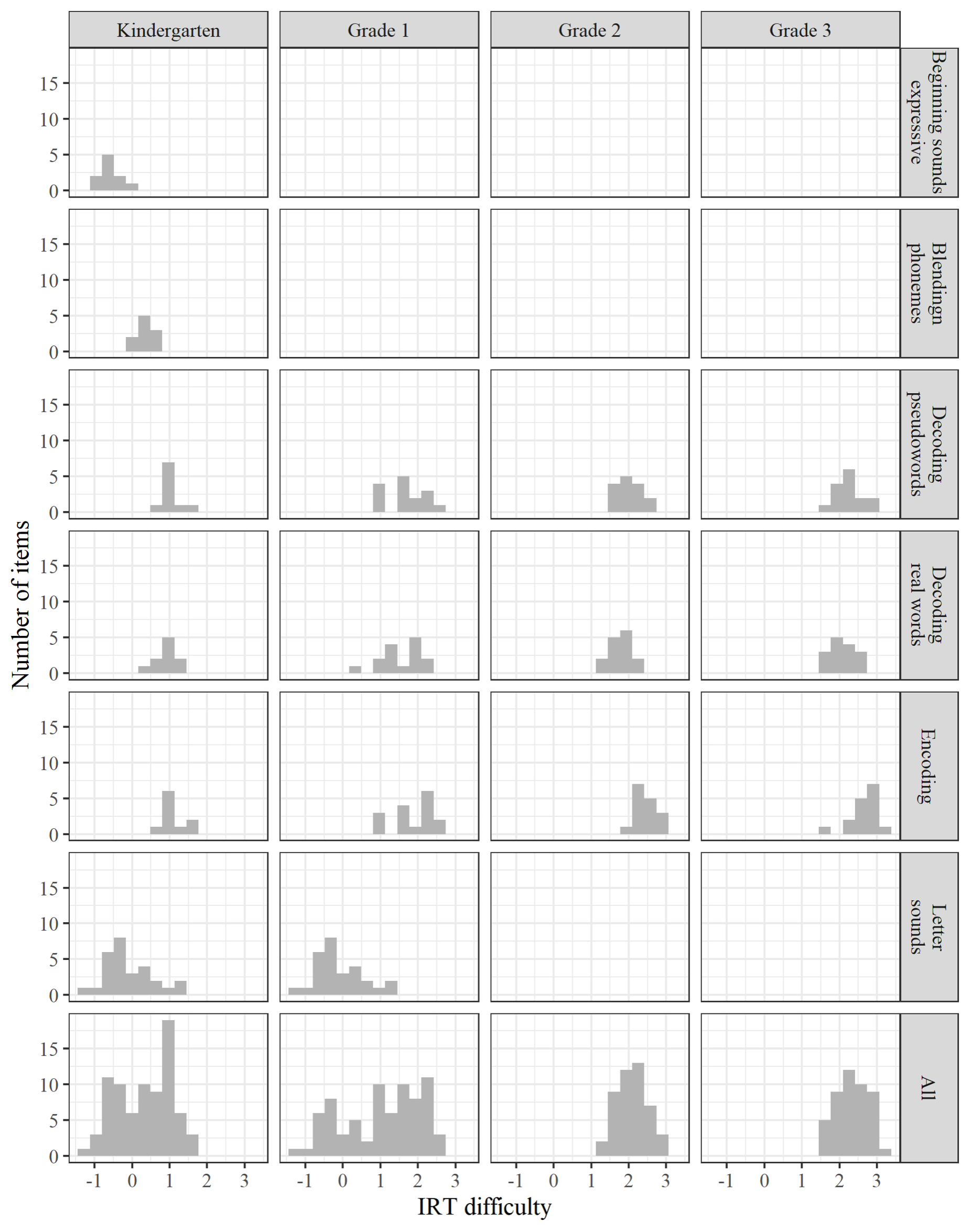
As another check on how we modeled item responses, we examined item parameters and their distributions by grade. The distributions of the item difficulty parameters shifted to the right as grade level increased, as seen in Figure 2. This indicates that the items included in the test form for a given grade level were typically more difficult than were items included in the test forms for lower grades. Figure 2 also shows the difficulty of items associated with each subtest for each grade. Within each grade (the columns in Figure 2), Letter Sounds items were easier than were Decoding items (real or pseudo words), and Encoding items were typically the most difficult. For Kindergarten, the phonemic awareness items (beginning sounds expressive and blending phonemes) were among the easiest. The within-ordering of these grades generally aligns with a priori theory on reading development. Though not depicted, the items at all grade levels appear to be adequately discriminating, as item discrimination values were typically between two and four.

Figure 2.
Item Difficulty Parameter Distributions by Subtest and Grade

Assumption 1.e: Items have consistent measurement properties for all tested students.

To determine whether VALLSS produced scores that are comparable for students in various demographic groups, we used multigroup CFA in which items were treated as binary to examine whether measurement invariance held across different student subgroups (estimated separately for each grade level). We used separate CFA models in which students were grouped by socioeconomic status, gender, race (we compared Asian, Black, and Hispanic students to white students), and English learner status. For each group comparison, we examined the fit statistics for two types of multigroup models: one in which all values were permitted to vary between groups (configural model) and one in which the loadings and thresholds were constrained to be equal between the two groups (scalar model). Given our large sample size, we opted not to use traditional chi-squared indicators of measurement invariance, which tend to be overpowered (Bagozzi, 1977; Bentler & Bonett, 1980; Yuan & Chan, 2016). Instead, we used the guidelines proposed by Cheung and Rensvold (2002), who stated that measurement invariance likely holds if the change in comparative fit index (CFI) is less than or equal to 0.010 and the change in root-mean-square errors of approximation (RMSEA) less than or equal to 0.015. Table 10 presents the CFI and RMSEA values for each model and the differences between those values by group and grade. We did not observe any groups for which the configural and scalar models differed enough to indicate failures of measurement invariance.

Table 10.
Measurement Invariance Fit Statistic Comparisons

Note. Conf. = Configural model, Scal. = Scalar mode, Diff. = Configural model – Scalar model
Note. The Asian, Black, and Hispanic groups were compared to non-Hispanic white students.

Inference 2: The VALLSS vertical scale allows us to compare student performance over time.

Tracking student growth over time is one of the primary intended uses of VALLSS. Consequently, we needed to ensure that the vertical scale adequately captures changes in student literacy skills across testing occasions, and that trends in those skills match what would be expected based on the science of reading. We begin with a description of the vertical scaling procedure used before turning to results employing the vertical scale.

Vertical Scaling Procedure

Perhaps the most common way to structure a study to develop a scale for grade-to-grade growth is with a common item nonequivalent groups design. This design involves administering common items to students in adjacent grades and using differences in their achievement levels to link each grade-specific scale across grades. For VALLSS, we too used a common item nonequivalent groups design. One of the most important features of a study using such a design is how many items should be used to link adjacent grades, with at least 20% of the items for a given grade’s form shared with the adjacent grade (Young & Tong, 2015). In our own study, a minimum of 30% of items for a particular grade were common with the adjacent grade.

Research also shows that decisions related to which items are common across grades can be consequential. In particular, Briggs and Dadey (2015) examined the impact of common item grade alignment when constructing a vertical scale. Specifically, they described “forward” and “backward” linking designs, corresponding to upper- and lower-grade common items. That is, psychometricians could include common items in adjacent grades by (a) including items from the upper grade in the lower grade’s test, (b) including items from the lower grades in the upper grade’s test, or (c) some combination of the two. Their results show difficulty estimates associated with different amounts of growth dependent on which approach was used, as items for the higher grades showed more instructional sensitivity than did those written for lower grade levels. Unsurprisingly, approaches that use a mix of items from both upper and lower grades tend to produce growth estimates in the middle, an approach we used in constructing the vertical scale for VALLSS. While VALLSS is not designed to strictly align with a specific curriculum, the SMEs who developed the test forms did consult the scope and sequence indicated by the Standards of Learning for the commonwealth of Virginia.

Once the design was established and item responses collected, we needed to select a calibration model. While we tested both concurrent and separate calibration approaches (all conducted using flexMIRT [Cai, 2017]), we ultimately settled on the concurrent approach. In the concurrent calibration, all grades were estimated in tandem using a multi-group model (with each group corresponding to a grade) in which cross-grade measurement invariance was imposed. The mean and SD of the lowest grade were constrained to 0 and 1 respectively, then the means and variances at older grades were freely estimated. To determine whether items functioned similarly across grade levels (which is relevant to the decision to constrain item parameters equal across grades), we calibrated a unidimensional IRT model for each grade separately and compared the estimated difficulty parameters of the linking items (Figure 3). The associations between these parameters were roughly linear for each pair of adjacent grades, providing some evidence that constraining the linking item parameters to be equal across grades would not result in a concurrently calibrated model with substantial misfit. (Results were also as expected when employing the linking parameters from the separate calibration to map item parameters onto each other in adjacent grades.)

Figure 3.
Associations Between Difficulty Parameters of Linking Items Produced Via Grade-Specific IRT Model Calibrations

Converting Scores from the Theta Metric to a Scale Score

Additionally, we wanted the reported scores to be easily interpretable by stakeholders. We decided to convert the raw theta scores into scaled scores by applying the following transformation:

Scaledscore =50×θ +550

This resulted in the score ranges present in Table 11. The minimum and maximum scores increase from grade to grade. Similarly, the ranges are fairly wide in kindergarten and narrow in the older grades. This aligns with the changes in means and variances described in the next section.

Table 11.
Scaled Score Ranges by Grade

Assumption 2.a: Patterns in score means and variances over time match a priori theory

Table 12 provides the means and variances for the theta values at each grade level. Students in higher grades do have higher scores, on average, than do students in lower grades. In line with what literacy experts on the project hypothesized, students made large gains between kindergarten and first grade as students were, in many cases, exposed to literacy instruction for the first time. Gains between subsequent grades then slowed as students mastered basic skills and moved on to increasingly subtle literacy skills.

Table 12.
Means and Variances of Theta Scores by Grade

Additionally, the variance in scores is lower for higher grade levels, which literacy experts also hypothesized would occur. As students are exposed to instruction, the variability in their skillsets decreases the longer the exposure. For example, in kindergarten, some students come in knowing how to read, while others have never been exposed to any kind of related instruction. This phenomenon produces large variability in the scores at kindergarten. However, as students with less exposure to reading are taught during kindergarten, they begin to catch up to their peers and the variability in literacy skills decreases.

Assumption 2.b: We do not observe notable floor or ceiling effects in student scores that may obscure student growth trends.

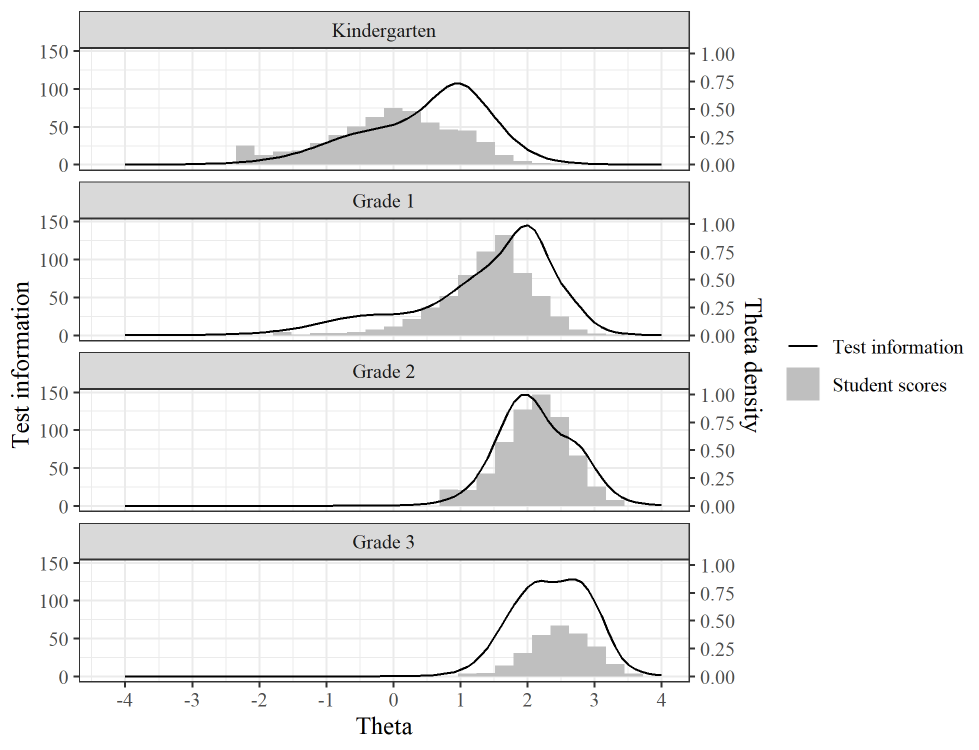
To allow stakeholders to adequately track student growth over time, the code-based tests needed to include a wide enough range of items to avoid floor or ceiling effects in student scores. In Figure 4, we see the student theta score distributions (gray histograms) alongside the test information curves (black lines) for each grade level. The test information curves, which indicate the places on the theta scale where the selected items on the test form provide the most information about student literacy, are well aligned with the student score distributions, particularly for the older grades. While the items included in the kindergarten test form are a bit more difficult than student scores suggest, there is still a good amount of alignment at the lower end of the score distribution. We do see some evidence of floor effects in kindergarten, and have tried to address such issues in subsequent test administrations (to the extent possible) by adding easier items.

Figure 4.
Test Information vs Student Scores

Inference 3: VALLSS scores can be used to accurately identify the students who are at risk of reading difficulties.

VALLSS scores will be used to identify students who are at risk of developing reading difficulties. It is, therefore, essential that the cutoffs used to assign students to the BOR are developmentally appropriate. Further, scores around those BOR must be reliable in order to help ensure accurate classification.

Assumption 3.a: Band of risk placements align with established criteria for appropriate developmental progress at each grade level

We used the bookmark method (Karantonis & Sireci, 2006) to establish developmentally appropriate score cutoffs for the three bands of risk for each grade. This method combines content knowledge and psychometrics, and the procedures were used to create score ranges for each band of risk. We relied on the item difficulty parameter for all of the retained code-based items. We also relied on six SMEs who brought considerable curricular knowledge, content area expertise, and teaching experience to bear on the decision-making process.

For the fall assessment term, SMEs were provided with a set of grade-specific lists of all code-based items that contribute to BOR designation. The items were listed in order from easiest to most difficult based on the item difficulty parameter. Because content area expertise was critical to this process, the lists included the subtest and the content for each item. SMEs were instructed to consider a number of statistics in combination with content area expertise when setting their suggested bands of risk including: the theta value of the items determined using IRT, the percent correct for the items (specific to grade level and term), the estimated quartile of the ranked items, and their knowledge of common appropriate scopes and, most importantly, sequences of reading and language content taught in K-3 classrooms. SMEs were encouraged to avail themselves of resources as needed and given time to independently identify the bookmarks.

The four SMEs first worked individually within the list for each grade to identify, or “bookmark,” the items that should serve as a cut-off for High Risk, Moderate Risk, and Low Risk designations. A facilitator next compiled the individual bookmarking to one file, which SMEs gathered to review. See Figure 5 for an example of completed list from one SME as well as an example of a list with four SME’s bookmarks compiled.

Figure 5.
Individual and Group SME Files

Note. Content redacted. Sample column labels are included to show how item-level information was shared with SMEs during the bookmarking process.

During SME meetings, the four SMEs viewed and discussed deidentified bookmarks together as one, with an additional two SMEs. Considerations about literacy development and local scope and sequence were revisited as needed, but within the context of VALLSS BOR. For example, the Letter Sounds and Letter Names subtests include all letters, as the literature tells us that letter sound identification is a historically reliable predictor of later reading ability; however, many kindergarten students will not know all of their letter sounds in the fall, and that is expected and accounted for via the band of risk. Through these discussions, the group agreed upon final fall, mid-year, and spring bookmarks for each grade.

Using the bookmarks set by the group of SMEs, we next mapped the difficulty values for those items back onto the vertical scale. This allowed us to create score ranges for each band of risk. Finally, these cut scores were transformed from the theta scale to the VALLSS scale score metric (Table 13). The same bookmarking process was repeated for mid-year and spring. Appropriate adjustments to the statistics specific to each assessment term were made (e.g., percent correct) and provided in a new set of grade-specific lists.

Table 13.
Band of Risk Score Ranges by Grade

Assumption 3.b: VALLSS scores are adequately reliable around band of risk cutoffs.

To ensure that students whose scores placed them near one of the cutoffs separating bands of risk were assigned to the correct band, we examined the standard errors in those locations. Figure 6 shows the standard errors for students by their theta score with vertical lines indicating the cutoffs between the bands of risk (note these standard errors are in the original theta metric, not the scale score metric). The standard errors are generally very low in those ranges of the vertical scale near the cutoffs, providing initial evidence that student scores are reliable enough to support placement.

Figure 6.
Standard Error by Theta

Inference 4: Implementing stop rules does not substantially alter students’ scores or risk designation

Given that the VALLSS test forms are fairly long, we aimed to shorten the test for some students by implementing stop rules. The items in each subtest are presented to students in order from least to most difficult. Given that students who do not answer the first (i.e., easiest) items correctly are unlikely to answer later items correctly, we allow teachers to stop administering items to a student if they do not answer any of the first 5 items correctly for code-based subtests and first 4 items correctly for language comprehension subtests. Our analyses showed that no more than 3% of students who answered these first items incorrectly would continue on to get even one correct item on the subtest, and only 0.5% of tested students would have a different band of risk designation if stop rule were implemented.

Assumption 4.a: Students who meet the stop-rule criteria earn the same scores whether they see all items or stop early

To determine the potential impact of stop rules, we used data from previous test administrations where all items were administered to the students, and we assessed how many student scores would change if stop rules were implemented at 4 or 5 consecutive questions wrong for each task, and if items were ordered from the easiest to the hardest observed difficulty (based on the average proportion correct). We found that stop rules would only change a small percentage of student scores for a given task, at most 3.09%. Furthermore, less than 0.5% of students in any given grade had their score across all tasks changed to zero if all stop rules were implemented.

Language-Based Tests

Most of the language-based subtests were time-based, which made it difficult to incorporate them into traditional measurement models. The items in the passage-based subtests, in which students read a short passage and answered questions about its contents, were the only ones that could be analyzed using more traditional means. Even so, we could not produce a vertically scaled score for these language subtests because students at each grade level were given different passages to read with no overlapping passages across grades. Consequently, we conducted a subset of the analyses performed for code-based skills, including item-total correlations, Cronbach’s alpha values, and CFA models for these sets of items separately for each grade. The correlations, alpha values, and CFA model fit statistics all met acceptable standards for use in operational testing when considered as correlated subtests, but a unidimensional model was not supported (See Table 14 for CFA fit statistics). A forthcoming chapter on score reporting will include the inferences and arguments for ORF, language comprehension items, and RAN, along with more detailed descriptions of these analyses.

Table 14.
Fit Statistics for Unidimensional and Subtest-based CFA Models for the Language Subtests